座標系の変換†
- ある座標系での運動がほかの座標系でどのように見えるかを知るには、座標系の変換が必要になります。
ガリレイ変換 (Galilean transformation)†
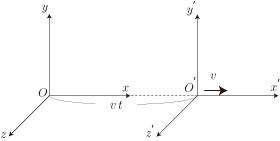
- ある座標系Aに対してx方向に速さvで運動する座標系A'での運動を考えましょう。ただし、座標系はどちらも慣性系とします。
- 座標系A'での座標(x',y',z')は、Aでの座標(x,y,z)と両者に共通の時刻tを用いて以下のように書けます。このような変換をガリレイ変換といいます。
x'＝x−vt
y'＝y
z'＝z
- 座標系A'での座標(x',y',z')は、Aでの座標(x,y,z)と両者に共通の時刻tを用いて以下のように書けます。このような変換をガリレイ変換といいます。
ローレンツ変換 (Lorentz transformation)†
- ガリレイ変換と同様に、ある座標系Aに対してx方向に速さvで運動する座標系A'での運動を考えましょう。ただし、座標系はどちらも慣性系とします。
- ガリレイ変換では特殊相対性理論の特殊相対性原理と光速度不変の原理を満たすことができません。
- 座標系A'での座標(x',y',z')と時刻t'は、Aでの座標(x,y,z)と時刻tを用いて以下のように変換する必要があります。このような変換をローレンツ変換といいます。
x'＝γ(x−vt)
y'＝y
z'＝z
t'＝γ(t−(v/c2)x)
ただし、γ＝1/sqrt(1−(v/c)2)
- このように、ローレンツ変換では空間と時間を一緒に変換する必要があります。したがって、時刻は座標系によって異なり、絶対的なものではありません。
- γをローレンツ因子(Lorentz factor)といいます。
- 速さvが小さければγはほぼ1であり、ガリレイ変換と同じになります。
- 速さvが光速cに近づくほどγは大きくなります。