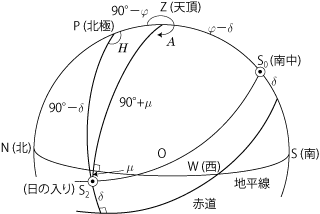
日の出・南中・日の入
世界地図と理科年表![[外部サイト]](/koyomi/image/extlink.png) ,それに簡単な電卓をもって1996年8月1日ハワイのマウナケア山にすばる望遠鏡を見学に行くことにした.地図からマウナケア山の経緯度は,λ= 西経155°30' ≡ -10.3667h (東経を+,西経を-),φ = 北緯19°50',山の高さは,h = 4206 mとわかる.まず,南中の時刻は
,それに簡単な電卓をもって1996年8月1日ハワイのマウナケア山にすばる望遠鏡を見学に行くことにした.地図からマウナケア山の経緯度は,λ= 西経155°30' ≡ -10.3667h (東経を+,西経を-),φ = 北緯19°50',山の高さは,h = 4206 mとわかる.まず,南中の時刻は
T = 12h - (λ - λ0) - ΔT ・・・(1)
λ0はハワイでの標準時の経度で,理科年表「世界各地の標準時」によれば λ0 = 西経150°≡ -10h,ΔT は均時差で,理科年表「太陽」の項から,8月1日世界時0hでは-6m18.1s,8月2日では-6m14.0s.ハワイ時間正午12h での値は比例配分して
ΔT = -6m18.1s + {12 - (-10)} / 24 ×{-6m14.0s - (-6m18.1s)} = -6m14.3s ≡ -0.1040h
T = 12h - {-10.3667h - (-10h)} - (-0.1040h) = 12.4707h ≡ 12h28.2m
出入りの時角
次に,日の出・日の入は,太陽の上辺が地平線に接する時をとり,また大気の屈折によって太陽自身が浮き上がって見えるので,図のように,地平線より μ だけ下にある時を計算する.図の ΔPS2Zより太陽の出入の時角 H は
cos H = -tan φ tan δ - sin μ sec φ sec δ ・・・(2)
ここで,μ は平均の値として51',δ は太陽の赤緯.再び,理科年表「太陽」の項にある8月1日と2日の赤緯から比例配分して
δ = +17°59' 56" + {12 - (-10)}/24 × (17°44' 41" - 17°59' 56") = +17°45' 57" ≡ +17.7658°
tan δ = 0.3204,tan φ = 0.3607,sec δ ≡ 1 / cos δ = 1.0501,sec φ = 1.0631,sin μ = 0.0148
cos H = -0.3607 × 0.3204 - 0.0148 × 1.0631 × 1.0501 = -0.1321
∴ H = 97.5910° ≡ 6h30.4m
出入りの時刻
ゆえに,日の出の時刻: T - H = 5h57.8m,日の入の時刻: T + H = 18h58.6mとなる.
高い所では日の出はより早く,日の入はより遅くなるが,その効果は
Δ
t = 0.140
m ×
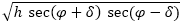
・・・(3)
Δ
t = 0.140
m ×
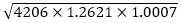
= 10.2
m
マウナケア山頂でみる日の出は 5h48m,日の入は 19h9m (ハワイ時) となる.また,方位角 A は北から東まわりに測って,図より
cos μ sin A = -cos δ sin H ・・・(4)
sin A = ±0.9523 × 0.9912 = ±0.9439 ( μ は小さいので cos μ ≈ 1 )
A = 70.7172° (日の出), 289.2828° (日の入)
すなわち,東または西の方向より,北へ19°の方向に日の出,日の入を見ることになる.
暦象年表1996より加筆、訂正
![]() ,それに簡単な電卓をもって1996年8月1日ハワイのマウナケア山にすばる望遠鏡を見学に行くことにした.地図からマウナケア山の経緯度は,λ= 西経155°30' ≡ -10.3667h (東経を+,西経を-),φ = 北緯19°50',山の高さは,h = 4206 mとわかる.まず,南中の時刻は
,それに簡単な電卓をもって1996年8月1日ハワイのマウナケア山にすばる望遠鏡を見学に行くことにした.地図からマウナケア山の経緯度は,λ= 西経155°30' ≡ -10.3667h (東経を+,西経を-),φ = 北緯19°50',山の高さは,h = 4206 mとわかる.まず,南中の時刻は