暦Wiki/振り子の等時性 - 国立天文台暦計算室

振り子の等時性 (isochronism of the pendulum)†

同じ長さの振り子がゆれる周期は、振り子の重さや(振れ幅が大きくなければ)振れ幅にはよらず一定になります。これを振り子の等時性といいます。
- 振り子の揺れた回数を数え、それに振り子の周期をかければ、その間の時間を測ることができます。
- これを利用した時計が振り子時計です。

振り子の周期をT[s]、振り子の長さをl[m]とすると、以下のような関係が成り立ちます。
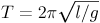
- gは重力加速度*1で、およそ9.8m s^-2の定数です。
- 振れ幅が大きくないときに近似的に成り立つ式です。
この式を逆に解くと、振り子の長さが求まります。
- 垂揺球儀は1日約60,000往復ですから、周期T[s]＝86,400÷60,000。したがって、振り子の長さl[m]＝9.8×(86,400÷60,000÷2π)²≈0.5m≈1尺7寸。
- 垂球は1日約35,000往復ですから、周期T[s]＝86,400÷35,000。したがって、振り子の長さl[m]＝9.8×(86,400÷35,000÷2π)²≈1.5m≈5尺。
この式から、振り子の長さが変わると周期が変わることがわかります。
- 金属製の振り子は熱膨張のため、温度によって伸びたり縮んだりします。これにより時計に進みや遅れが生じます。
  - 熱い時には振り子は伸び、周期が長くなります。したがって、時計の針は遅く動きます。
  - 寒い時には振り子は縮み、周期が短くなります。したがって、時計の針は速く動きます。
- なお、星学手簡の寛政十年五月九日付の手紙(p.50)で間重富が昼夜の違いについて述べていますが、寒いときに回転が悪くなり、ろうそくを近づけると回転がよくなるというので、まったく別の問題のように思われます。