算術†
- 授時暦で用いられた新たな計算手法は、暦学者のみならず、数学者にも多大な影響を与えました。
- 和算で有名な関孝和、その弟子で徳川吉宗のブレーンとなった建部賢弘など、多くの学者が授時暦を研究しています。
弧背術†
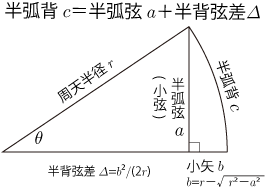
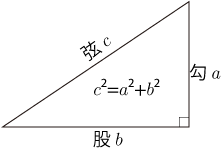
- 弧背術とは、三角関数の代わりに用いられた近似計算のことです。
- 関孝和『授時発明』など、一般的には円周率 π=3とし、2πr=365.25度(周天)より、周天半径 r=60.875度を用いています。
- たとえば、下図において、
- 逆に、半弧背cを与えて小矢bを解くには、bについての4次方程式を解く必要があります。
b4+4r(r-c)b2-8r3b+4r2c2=0