図1:惑星の等級
2022年版暦象年表では,Mallamaら1の成果をもとに,惑星の等級算出方法を見直した.1986年版以降,長らくHarrisの式2をベースにしたものを用いてきたので,久しぶりの改訂となる.

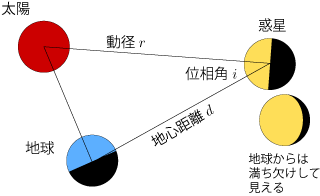
惑星は太陽の光を反射して輝いて見えるので,太陽から惑星までの距離=動径 r が大きくなるほど,惑星から地球までの距離=地心距離 d が大きくなるほど暗くなる.また,太陽・惑星・地球の位置関係により輝いて見える部分が変化=満ち欠けすることでも,明るさが変化する.後者の影響を太陽-惑星-地球のなす角=位相角 i の関数 Δm(i) で表すと,惑星の等級 V は,
V = V (1, 0) + 5 log10 rd + Δm(i)
のようになる.ここで,V (1, 0) は r = 1 au,d = 1 au,i = 0°における V の値である.Δm(i) には位相角 i が0に近づく際に急激に明るさを増す現象,いわゆる衝効果3も含まれている.さらに,惑星の地表や大気における光の反射具合は一様ではないので,惑星の自転軸の向きや自転量,大気の状態などによっても明るさは変化する.
以下,惑星ごとに新旧の値を比較していこう.
まず,水星と金星については,SOHO (Solar and Heliospheric Observatory) の観測成果により,内合や外合付近での振る舞いが大きく改善された.水星は外合における衝効果が鋭くなったほか,内合付近もより暗いところまで表せるようになった.また,金星は極大等級の値や内合前後 (位相角 i ≈163°) での増光現象についても改善されている.この増光現象は金星大気中の硫酸分子による前方散乱が原因と考えられている.
なお,外合・合の直前直後は太陽に近づくため,内合の直前直後はそれに加えて輝く面がほとんど見えなくなるため観測困難であり,Mallamaらの式も適用範囲外ではある.しかし,参考値としては支障ないと思われるので,暦象年表ではこれまで通り拡大適用して算出・掲載することとした4.
火星についても衝効果が改善されたほか,自転軸の向きと自転量に伴う周期項が加わった.ただし,火星の自転周期は地球とほぼ同じで1日ごとの数値を掲載しても正しく補間できないことから,暦象年表では自転量に伴う周期項は省いている.この,自転量による影響は砂嵐の影響とあわせても±0.1等程度である.
木星については,大きな違いは見られない.土星については,土星の環による衝効果が鋭くなった.この効果は土星の環が傾いて見える時ほど大きく,現在は2025年の環の消失に向けて徐々に小さくなりつつある.
天王星については自転軸の向きに伴う周期項が加わった.天王星の自転軸は公転面に対してほぼ横倒しになっており,極域が太陽を向いている時期は赤道が太陽を向く時期に比べて0.07等ほど明るくなる.極域のほうが明るいのは,赤道域に比べてメタンの占める割合が低く,メタンによる光の吸収が抑えられるためと考えられる.海王星については1980年ごろから2000年ごろにかけて等級が徐々に変化し,0.1等ほど明るくなった.この原因は海王星の季節変動による可能性もあるが,はっきりしない5.
1) Mallama, A and Hilton, J.L., Computing apparent planetary magnitudes for The Astronomical Almanac, Astronomy and Computing, 25, 10 (2018). → 本文(1)に戻る
2) Harris D.L., Photometry and colorimetry of planets and satellites, Planets and Satellites edited by Kuiper G.P. and Middlehurst B.M., The University of Chicago Press, 272 (1961). → 本文(2)に戻る
3) 衝のときに発見されたので衝効果という名前で呼ばれるが,合のときでも見られる.→ 本文(3)に戻る
4) 英米暦 (The Astronomical Almanac 2021) では,水星については 2.1°< i < 169.5°,金星については 2.2°< i <179.0°のみ有効,そこから外れるものは無効で,「-」と記載されている.→ 本文(4)に戻る
5) 参考: 海王星は思ったより冷たい (すばる望遠鏡) → 本文(5)に戻る
暦象年表2022より