Glossary

Geocentric Coordinates of Celestial Bodies

Apparent Right Ascension (R.A.), Apparent Declination (Dec.), Apparent Longitude (Lon.), Apparent Latitude (Lat.)

These values are with respect to true equator and true equinox of date. Aberration is included.

Geocentric Distance (Dist.)

Geocentric distance is the true distance between the celestial body and the Earth, scaled by the astronomical unit (au, 1 au = 149,597,870.7 km). In case of the Moon, it is scaled by the mean distance between the Moon and the Earth, i.e. 384,400km.

Parallax

Parallax is the equatorial horizontal parallax Π and sin π = (equatorial radius of the Earth) / (distance between the object and the Earth).

Apparent semi-diameter (S.D.)

The apparent semi-diameter of the Sun at 1 au is 16' 1.18". The apparent semi-diameter "s" of other objects is determined by sin s = (equatorial or polar radius of the objects) / (distance between the object and the Earth).

Astrometric position (R.A.^*, Dec.^*)

Astrometric position is useful for comparing dim objects like dwarf planets or asteroids directly with star catalogues and star charts.

The H-G Magnitude System, which was adopted by IAU Commission 20 in 1985, is used for these small objects.

Heliocentric Coordinates of Celestial Bodies

Heliocentric Longitude (Lon.), Heliocentric Latitude (Lat.)

These values are with respect to mean equator and equinox of date. Aberration is not included.

Radius

Radius is the distance between the object and the Sun, scaled by the astronomical unit (au, 1 au = 149,597,870.7 km).

Orbital Longitude, Daily Motion

Orbital Longitude is measured from equinox to ascending node along the ecliptic and then from ascending node to the object along the orbit, in other words, sum of the longitude of the ascending node and the argument of perihelion. Daily motion is the amount of change in orbital longitude for one day.

Rotation of the Sun

Rotation of the Sun

From the motion of sunspots on the solar sphere, one can notice the Sun rotates along some kind of axis. The direction of this rotation axis is 19^h5^m, +63.9°. The cycle of rotation against the Earth is 27.2753 days and the cycle against stars is 25.38 days. (Carrington Period; Heliographic latitude around ±16°)

The position of the rotation axis

In "Rotaition of the Sun", P is the position angle of the solar axis from celestial north, positive being eastward and negative being westward. B₀ and L₀ are heliographic latitude and longitude of the Earth, respectively. Heliographic longitude 0° is the solar meridian which passed the ascending node of solar equator against the ecliptic at noon on Jan. 1, 1854 (GMT). The values P and B0 become almost identical after 4 year periods.

Rotation of the Moon

The position of the rotation axis

P is the position angle of the rotation axis from celestial north, positive being eastward and negative being westward.

B₀ and L₀ are selenographic latitude and longitude of the Earth, respectively. Selenographic Coordinates refer to the mean Earth/polar axis system i.e. ME system.

The direction of the Sun

Bs and Ls are selenographic latitude and longitude of the Sun, respectively. Ps is the position angle of the direction of the Sun measured from celestial north, positive being eastward and negative being westward.

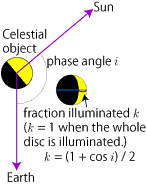i is the Sun - Moon - Earth angle called phase angle. k shows the ratio of the illuminated part per diameter of the Moon called fraction illuminated. k = (1 + cos i) / 2, i.e. k = 1 when i = 0° and k = 0 when i = 180°.

However, since the orbit of the Moon is a little bit inclined with respect to the ecliptic, these cases will basically not occur. If i gets close to 0° or 180°, you should meet lunar eclipse and solar eclipse, respectively.

Rotation of the Planets

The position of the rotation axis

P is the position angle of the rotation axis from celestial north, positive being eastward and negative being westward. North pole of the axis lies in the same side as the north pole of the Earth with respect to the invariable plane of the Solar System.

B₀ and L₀ are planetographic latitude and longitude of the Earth, respectively. Flattening of the planet is included for planetographic latitude and planetographic longitude increases as the planet rotates.

The 20° meridian for Mercury is defined by the crater Hun Kal. The 0° meridian for Venus is defined by the central peak in the crater Ariadne. The 0° meridian for Mars is defined by the crater Airy-0. (More precisely, the longitude of the Viking I lander is defined to be 47.95137° west, so that the crater Airy-0 remains on 0°.) Meridian for Jupiter, Saturn, and Uranus refers to its own magnetic field i.e. System III, and meridian for Neptune refers to the optically observed features in the Neptunian atmosphere i.e. System II.

The direction of the Sun

Bs and Ls are planetographic latitude and longitude of the Sun, respectively. Ps is the position angle of the direction of the Sun measured from celestial north, positive being eastward and negative being westward.

i is phase angle and k is fraction illuminated. (See the figure in "Rotation of the Moon".)

λs is the solar longitude in the ecliptic of the planet and is measured from the ascending node of planet's ecliptic against planet's equator i.e. planet's equinox.

Greenwich Sidereal Time

Greenwich Apparent Sidereal Time, Greenwich Mean Sidereal Time, Equation of Equinoxes

Greenwich Apparent Sidereal Time (GAST), Greenwich Mean Sidereal Time (GMST) are sidereal time with respect to true equinox and mean equinox, respectively. Equation of equinoxes is nutation in right ascension and GAST = GMST + Equation of equinoxes.

Equation of Time

Equation of Time = Hour angle of apparent Sun - Hour angle of mean Sun.

Julian Date

Julian Date

Julian date is days passed from noon on Jan. 1, 4713 B.C.. In "Julian Date" and "Julian Date -> Calendar Date", the year before 1 A.D. is year 0.

Julian calendar and Gregorian Calendar

Seasons repeat themselves with a period called tropical year or 365.2444 days, which corresponds to 1 revolution of the Earth around the Sun. In Julian calendar, leap year i.e. year with 366 days is introduced once in 4 years in order to keep up with 1 tropical year.

Since the mean length of a Julian calendar year is 365.25 days, the difference between Julian calendar year and the tropical year grows 3 days after 400 years. In 1582, Pope Gregory XIII made years which can be divided by 100 and not by 400 to be a common year and the next day after Oct. 4th, 1582 to be Oct. 15th, 1582. This new calendar is the Gregorian calendar, which is still a standard calendar today.

Time System

JCST, Japan Central Standard Time

JCST is the official Time System in Japan. JCST = UTC + 9 hours. Sometimes JCST is called JST, Japan Standard Time.

UT, Universal Time

UTC = UT1 - ΔUT1 and ΔUT1 is determined from observation. In case of "Calendar and Ephemeris", ΔUT1=0. UTC is adjusted with leap seconds to keep ΔUT1 ≤ ±0.9^s.

TT, Terrestrial Time

TT is Geocentric Coordinate Time × constant value, so that its unit is exactly 1 SI second. It is almost the same as Geocentric Dynamical Time. TT = UT1 + Δ T, which should be determined by observation.