恒星時について

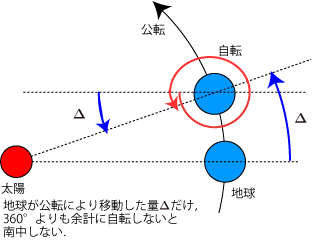
すべての星が北極星を中心に1日かけて回転しているように見えるのは，地球が1日約360°という速さで自転しているためにほかならない．1日という概念は太陽が南中してから次に南中するまでの時間とおおよそ考えてよいのだが，地球はその間にも公転により移動するので実際には360°自転するだけでは足りず，図１のように移動した量Δだけ余計に自転しなければならない．一方，十分に遠方の恒星にとってはΔは無視できるから，360°自転すれば再び南中する．前者のように太陽の南中を基準に考えた日や時刻が (太陽) 日・(太陽) 時，後者のように恒星の南中を基準に考えた日や時刻が恒星日・恒星時というわけだ．

地球の自転軸と恒星時

さらっと説明してみたものの，事はそう単純ではない．地球の自転軸は歳差・章動によって絶えず変動しているため，ある恒星に対して360°回転しても他の恒星に対してはまだ足りないという状況が発生してしまうのだ．このため恒星時は春分点を使って定義することになっている．つまり，グリニジ恒星時0^hに春分点が本初子午線に南中し，それから1恒星日＝24恒星時間後に再び南中するという具合である．なお，恒星年と太陽年の場合とは恒星・太陽といった言葉の使い方が若干異なる¹ので注意されたい．

平均恒星時と視恒星時

春分点に平均春分点と真春分点があるように，恒星時にも平均春分点をもとにしたグリニジ平均恒星時と真春分点をもとにしたグリニジ視恒星時がある．両者の差は分点均差と呼ばれ，赤経における章動を表している．このように，恒星時は地球の自転に似た概念ではあるものの，歳差や章動の影響を含んだものになっている．

恒星時と世界時の関係

さて，1太陽年経つとΔの累計はちょうど360°に達する．つまり，365.2422 (太陽) 日 = ( 365.2422 ＋ 1 ) 恒星日，すなわち1恒星日 = 365.2422 ÷ ( 365.2422 ＋ 1 ) 日≈ 23時間56分となり，1恒星日は24時間よりも4分ほど短いことがわかる．わずかな違いだが，これゆえに同じ時刻に見える天体がゆっくりと変化していくことになる．

逆に，1日 = ( 365.2422 ＋ 1 ) ÷ 365.2422 恒星日 ≈ 1.0027379恒星日であるから，恒星時は世界時よりも1.0027379倍速く進む．本書には世界時 0^h における恒星時 Θ₀ が掲載されているが，任意の世界時 (UT1) における恒星時 Θ を求めるには，Θ = Θ₀ ＋ 1.0027379 × UT1 とすればよい．0^h の値から補間することも可能であるが，恒星時は1日で一回りしてしまう量であるので，表値にその分を加味してから補間をする必要がある．

恒星時の歴史

歴史的にみれば，水晶時計や原子時計のように十分な精度の時計が登場するまでは，むしろ天体の子午線通過を観測して恒星時を求め，それをこの関係を使って変換し，時計を合わせていた．いわゆる平均太陽時である．太陽の動きは地球の運動にもとづくものであり，実際の太陽を観測しても季節によらず一様な時刻系を作ることはできない．ゆえに，恒星を観測することで実現するわけだ．実際の太陽の動きに基づく時刻 (視太陽時) と一様な時刻 (平均太陽時) の差は均時差 (図２) と呼ばれる．

図３：天体の時角

恒星時の役割

時角

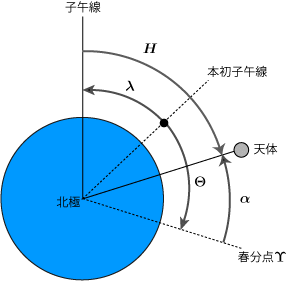
恒星時によって本初子午線と春分点の関係がわかれば，地上の世界 (地平座標系) と天体の世界 (赤道座標系) を結びつけることが可能になる．経度λにおける子午線から赤経αの天体まで測った角距離，すなわち天体の時角 H の大きさは図３のように，

H = Θ ＋ λ － α

となる．天体の高度・方位や出入り時刻など，さまざまな天文現象はこの時角 H を用いて算出すればよい．

図４：地平座標系と赤道座標系

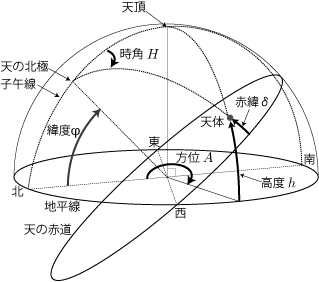
たとえば，緯度φ・経度λの地点における，赤経α・赤緯δの天体の高度 h ・方位 A は，時角 H を用いて以下のように算出する．

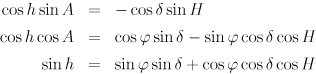
時角 H が 0 になるということは天体が子午線上にあること，すなわち日本付近の緯度なら天体が南中することを意味する．実際に上式に H = 0 を代入すると，方位 A = 180 °(つまり南)，南中高度 h = 90° － φ ＋ δ が得られる．

天体の位置

また，地心から見た天体の位置と緯度φ・経度λの地点から見た天体の位置のずれ，すなわち地心視差も，簡易的には時角 H を用いて以下のように観測地における時角 H′ と赤緯 δ′ を算出すればよい²．

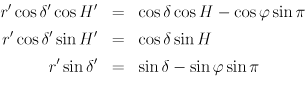
ここで，πは天体の赤道地平視差であり，地球の赤道半径を a_E ，天体の地心距離を r とすると sin π = a_E / r のように表せる．地心視差は天体の高度が低い時ほど大きく，最大で赤道地平視差にほぼ等しくなる．十分遠くにある天体ではあまり問題にならないが，月の場合は約1°すなわち月丸2個分にも達するので必ず補正しなければならない．

備考

1) 恒星年は固定座標系を基準として地球が1公転する時間，太陽年は春分点を基準として1公転する時間 →本文(1)に戻る

2) r′ はその地点から天体までの距離と地心から天体までの距離の比を表す．→本文(2)に戻る

恒星時とは