暦Wiki
太陽時と恒星時†
太陽日と恒星日†
- 恒星時が春分点に対する地球の自転量を表すのに対し、太陽時は太陽に対する地球の自転量を表します。
- いわゆる1日は太陽時で24時間に相当し、これを太陽日と呼びます。同様に恒星時で24時間のことを恒星日と呼びます。
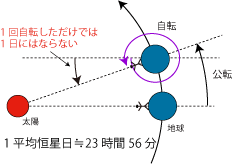
- 地球が公転によって動いた分だけ、太陽日は恒星日よりも長くなります。
太陽時と恒星時の関係†
- 地球が公転で動いた分だけ、両者は異なります。この量は季節によって変化します。
- 動いているものの自転量は理解しづらいと思いますで、地球を中心に春分点方向を固定した図を描くと、以下のようになります。
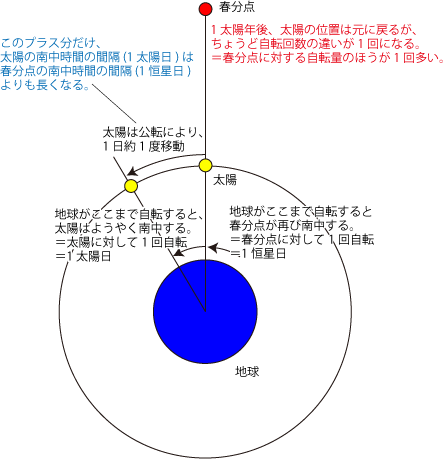
- 地球は春分点に対して1恒星日に1回自転します。
- 地球は太陽に対して1太陽日に1回自転します。公転のため太陽の位置は移動しますから、1恒星日よりも長くなります。
- 1太陽年〜365.2422太陽日だけ経過すると、太陽の位置は元に戻ります。
- このとき、太陽に対する自転の回数は365.2422回です。
- 春分点に対する自転の回数はこれよりも1回多く、366.2422回です。
- したがって、1恒星日=春分点に対して1回自転するのにかかる時間は平均的に365.2422太陽日÷366.2422回≒23時56分となります。
- 平均の長さはそれぞれ、平均恒星日、平均太陽日と呼びます。すなわち、平均恒星日=平均太陽日×365.2422÷366.2422です。
- 両者の差は約4分です。これにより恒星の南中時刻は毎日約4分ずつ早まり、季節の星座が変化していきます。
- 1太陽年で、恒星時は太陽時よりも366.2422回÷365.2422回≒1.0027379倍速く進んでいます。
- つまり、恒星時の変化量をΔΘ、太陽時の変化量をΔUTとすると、平均的にΔΘ=1.0027379ΔUTが成り立ちます。
- 恒星の子午線通過を観測して恒星時を求め、この関係式を使って太陽時に変換すると、公転に伴う季節変動を除去できます。これが平均太陽時です。
- 逆に平均太陽時がわかっていれば、この関係式で恒星時を求めることができます。
- すなわち、平均太陽時0時における恒星時をΘ0とすると、平均太陽時UTにおける恒星時ΘはΘ=Θ0+1.0027379 UTとなります。
関連ページ†
Last-modified: 2020-07-28 (火) 17:51:46

