暦Wiki
ケプラー (Kepler) の法則†
- ヨハネス・ケプラー (1571-1630、ドイツ) の発見した、惑星の運動に関する法則のこと。このため惑星の運動をケプラー運動と呼ぶこともあります。
- これらの法則を数学的にまとめあげたのが、ニュートンの万有引力の法則です。
ケプラーの第1法則†
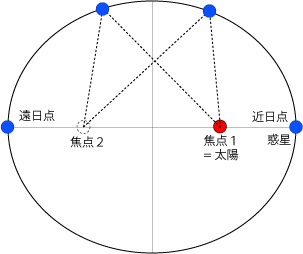
- 惑星は太陽を1つの焦点とする楕円軌道を公転します。
- 太陽は楕円の中心ではなく、少しずれた焦点に位置します。
- 惑星と太陽が最も近づく近日点、最も遠ざかる遠日点、太陽 (焦点) はすべて楕円の長軸 (長い方の軸) の上にあります。
- 軌道長半径をa、離心率をeとすると、最近距離はa(1-e)、最遠距離はa(1+e)となります。
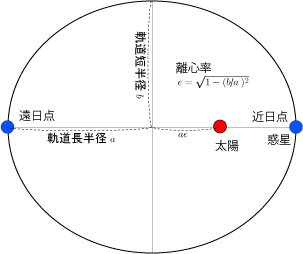
- 軌道長半径 (長い方の軸の半径) をa、軌道短半径 (短い方の軸の半径) をbとしたとき、
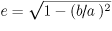 を離心率といいます。
を離心率といいます。
- 離心率が0のときは円、離心率が大きくなるほど楕円はつぶれ、離心率が1のときは放物線をあらわします。
ケプラーの第2法則†
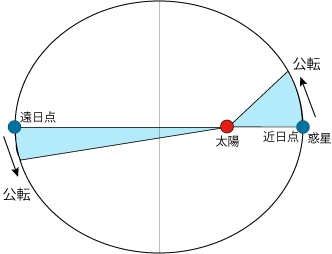
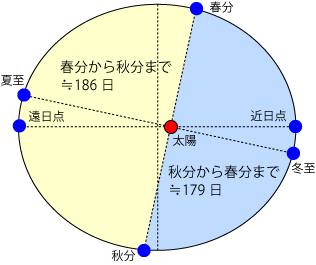
- 惑星と太陽を結ぶ線が一定時間に描く面積(黄色の部分)は等しい。
- このため太陽から近い所では速く、遠い所では遅く動きます。
- 面積速度一定の法則とも言います。
- 逆に、「面積が等しければかかる時間は等しい」「面積が大きければかかる時間は長く、小さければかかる時間は短い」ともいえます。
- このため、楕円軌道上のある地点Aから180°反対の地点Bに行くのにかかる時間と、地点Bから地点Aに行くのにかかる時間は一般に等しくなりません。
- より一般的には角運動量保存則にまとめられます。
ケプラーの第3法則†
- 惑星の公転周期の2乗は軌道長半径の3乗に比例します。
- 内側にある (太陽に近い) 天体ほど速く、外側にある (太陽から遠い) 天体ほど遅く動きます。
- 惑星の種類や楕円のつぶれ具合には依存しません。

関連ページ†
Last-modified: 2022-07-12 (火) 20:42:01
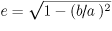 を離心率といいます。
を離心率といいます。




