暦Wiki
太陰太陽暦 (Lunisolar calendar)†
- 旧暦とは、厳密には明治五年まで用いられていた天保暦法による暦を指します。
- これに対し、現在使われている太陽暦 (グレゴリオ暦) は新暦と呼ばれます。
- 旧暦明治五年十二月三日を新暦明治6年1月1日としました。これにちなんで、12月3日はカレンダーの日と呼ばれています。
- 暦の変更は混乱も伴いますので、明治6年の改暦後も明治42年暦まで旧暦併記が続きました。
- 旧暦は既に廃止され、天保暦の手順どおりに推算・公表する機関はありません。
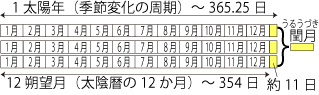
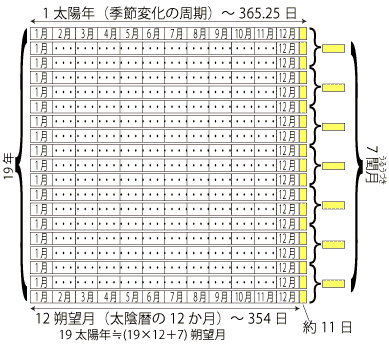
19年周期†
- 19年 (章法、メトン周期 Metonic cycle)
- 平均的な1年の長さが太陽年に近づくよう、19年に7回うるう月を挿入します。いわゆる十九年七閏です。
- 365.2422×19≒ 29.530589×(19×12＋7)
- 19年後の月の満ち欠けはほぼ同じになります。
- 古代中国暦では19年を1章と呼び、この周期に従ってうるう月を挿入していました。これを章法といいます。
- 四分暦では1太陽年＝365.25日としており、1朔望月＝365.25×19÷(19×12＋7)≒29.53085日となります。
- あくまで近似的な関係ですから、後にはこれに従わずより正確な暦法が現れます。これを破章法と呼びます。
- 76年 (カリポス周期 Callipic cycle)
- ユリウス暦や四分暦のように1年の長さを365.25日とすると、19年ではうるう年の周期が循環しません。
- そこでその4倍の76年をとることで、76年に28回うるう月を挿入することにしたものです。
- つまり、1朔望月＝365.25×76÷(76×12＋28)＝29＋499/940≒29.53085日です。
- メトン周期とカリポス周期はどちらも太陽年/朔望月＝235/19であり、中国暦法的には章法に分類されます。古代ギリシャの天文学者ゲミノスに沿って整理すると、
- メトン周期は、
- 19太陽年＝235朔望月は小の月110個と大の月125個、すなわち110×29日＋125×30日＝6940日。
- ここから、1太陽年＝6940÷19＝365+5/19日、1朔望月＝6940÷235≒29.5319日となります。
- これらの数値はAntikytheraの機械でも確認することができます。
- カリポス周期は、メトン周期の4倍から1日減らし、
- 76(＝4×19)太陽年＝940(＝4×(19×12＋7))朔望月＝(4×110＋1)×29日＋(4×125−1)×30日＝27759日。
- ここから、1太陽年＝27759÷76＝365.25日、1朔望月＝27759÷940≒29.53085日となります。
- 同様に、ヒッパルコスは1年の長さを365.25日より1/300日短いとしたので、さらに4倍して1日減らし、
- 304(＝4×4×19)太陽年＝3760(＝4×4×(19×12＋7))朔望月＝(4×(4×110＋1)＋1)×29日＋(4×(4×125−1)−1)×30日＝111035日。
- ここから、1太陽年＝111035÷304＝365.24671日、1朔望月＝111035÷3760≒29.530585日となります。
その他の周期†
- 8年 (Octaeteris)
- 365.25×8＝2922日＝(29＋30)×6×8＋30×3という関係から、8年の間にうるう月を3回入れるというものです。
- 1朔望月＝365.25×8÷(8×12＋3)＝29＋51/940≒29.51515日と、あまり精度はよくありません。
- 84年
- 76年＋8年の周期です。
- 1朔望月＝365.25×84÷(84×12＋31)＝29＋550/1039≒29.529355日と、あまり精度はよくありません。
- ただし、365.25×84＝30681日が7の倍数であり、曜日が元に戻るという利点があります。
- ローマ派がイースターの決定に用いていました。
- 25年
- 古代エジプトではうるう年のない365日の太陽暦が用いられていました。
- 1朔望月＝365×25÷(25×12＋9)＝29＋164/309≒29.530744日となります。
関連ページ†
